Local supply side
$$ \newcommand{\tsum}{\textstyle\sum} \newcommand{\extern}[1]{\mathrm{\mathbf{{#1}}}} \newcommand{\local}{\mathrm{local}} \newcommand{\roc}[1]{\overset{\scriptsize\Delta}{#1{}}} \newcommand{\ss}{\mathrm{ss}} \newcommand{\aa}{\mathrm{aa}} \newcommand{\bb}{\mathrm{bb}} \newcommand{\E}{\mathrm{E}} \newcommand{\ref}{{\mathrm{ref}}} \newcommand{\blog}{\mathbf{log}\ } \newcommand{\bmax}{\mathbf{max}\ } \newcommand{\bDelta}{\mathbf{\Delta}} \newcommand{\bPi}{\mathbf{\Pi}} \newcommand{\bU}{\mathbf{U}} \newcommand{\newl}{\\[8pt]} \newcommand{\betak}{\mathit{zk}} \newcommand{\betay}{\mathit{zy}} \newcommand{\gg}{\mathrm{gg}} \newcommand{\tsum}{\textstyle{\sum}} \newcommand{\xnf}{\mathit{nf}} \newcommand{\ratio}[2]{\Bigl[\textstyle{\frac{#1}{#2}}\Bigr]} \newcommand{\unc}{\mathrm{unc}} \notag $$
-
Several pairwise stages of production
-
Input factors
- Labor
- Intermediate imports
- Commodity inputs
- Capital
-
Real flexibilities to flatten the marginal cost schedule
- Variable utilization of capital
- Roundabout production
-
Production function with time-varying elasticity of substitution
![[math.md]]
Productivity
Global productivity component
Area-specific relative productivity component
Total area productivity
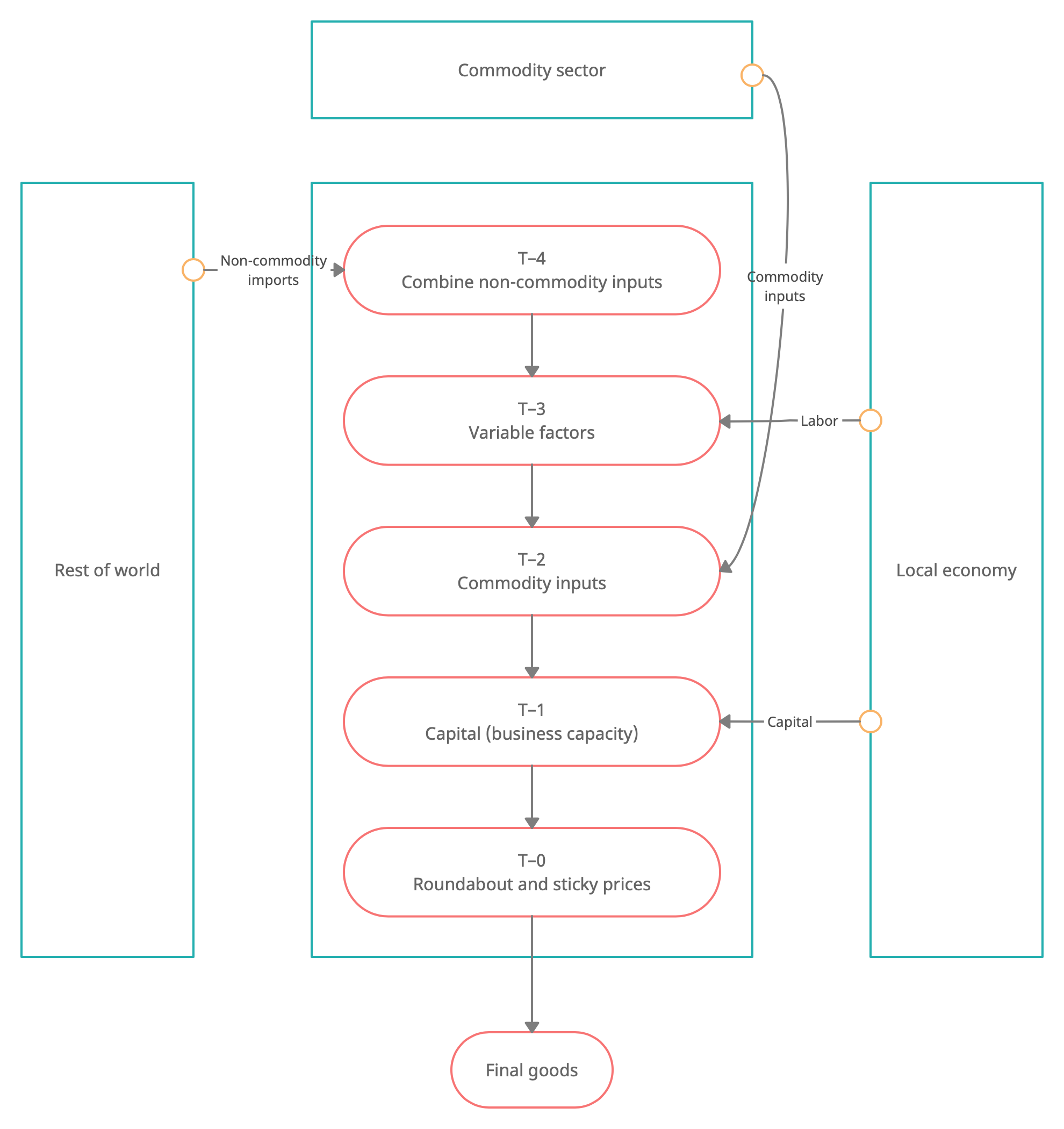
Production stages
Stage \(T-4\): Combine imports from the rest of the world
Production function with time-varying elasticity of substitution
where
-
\(my_t\) is the intermediate import inputs into local production
-
\(mx_t\) is the intermediate import inputs into export production (re-exports)
Stage \(T-3\): Combine non-commodity variable factors
Production function with time-varying elasticity of substitution
where
- \(nv_t\) is the variable labor input with \(\gamma_{nv} nh_\ss\) being the overhead labor needed to maintain production regardless of the output actually produced
Stage \(T-2\): Combine variable factors with business capital
Stage \(T-1\): Add dependence on commodity inputs
- Short-term: No elasticity of substitution (Leontief)
- Long-term: Unit elasticity of substitution (Cobb-Douglas)
Stage \(T-0\): Sticky prices
Total profits
Total profits summed up across all production stages are given by
Final goods
The final goods produced domestically are demanded as one of the following types of goods
-
Private consumption (by households), \(ch_t\)
-
Government consumption, \(cg_t\)
-
Private investment (by households), \(ih_t\)
-
Inputs into export production, \(yx_t\)
The market clearing conditions is therefore given by
GEES Local production module
Declare quantities
!variables(:production)
"Area specific productivity component" ar
"Shadow value of household budget constraing" vh
"Price of private consumption" pc
"Price of private investment" pih
"Domestic intermediate inputs" yz
"Stage T-3 output" y3
"Stage T-2 output" y2
"Stage T-1 output" y1
"Stage T-0 output" y
"Price of stage T-3 output" py3
"Price of state T-2 output" py2
"Price of state T-1 output" py1
"Price of stage T-0 output" py0
"Price of commodity input into production" pq
"Commodity input into production" mq
alpha_mq, alpha_y2
"Variable labor input into production" nv
"Nominal GDP" ngdp
"Real GDP index, Y/Y" roc_gdp
"Per-capita real GDP index, Y/Y" roc_gdp_to_nn
"Price of domestic production" py
"Nominal household rate, LCY" rh
"Price of final domestic output, Y/Y" roc_py
"Price of final domestic output, Y/Y, Point of reference" ref_roc_py
"Price of consumer goods, Y/Y" roc_pc
"Utilization rate of production capital" u
"Stage T-3 output, Y/Y" roc_y3
"Variable labor, Y/Y" roc_nv
"Auxiliary variable for steady-state calibration of upsilon_0" upsilon_1_py_to_pu
"Auxiliary equation for steady-state calibration of nu_0" nch_to_netw_minus_nu_0
Control log-status of variables
-
If a variable is growing at a nonzero rate in steady state then it must be declared as a log-variable
-
If a variables is changing by a constant in steady state then it must not be declared as a log-variable
-
If a variable can be negative, then it must not be declared as a log-variable
-
If there is conflict between rules 1 and 3, redefine the variable as ratio (so that the ratio is stable in steady state), and do not declare the ratio as a log-variable
!log-variables !all-but
zh, nch_to_netw_minus_nu_0
!parameters(:production :steady)
"S/S Area specific productivity component !! $\mathit{ar}_\ss$" ss_ar
"Share of overhead labor !! $\gamma_\mathit{n0}$" gamma_n0
"Share of intermediate imports in stage T-3 production !! $\gamma_m$" gamma_m
"Share of capital services in stage T-2 production !! $\gamma_\mathit{uk}$" gamma_uk
"Share of commodity inputs in stage T-1 production !! $\gamma_mq$" gamma_mq
"Share of roundabout intermediates in stage T-0 production !! $\gamma_\mathit{yz}$" gamma_yz
"Monopoly power (markup) of local producers !! $\mu_\mathit{py}$" mu_py
"Markup to cover overhead labor !! $\mu_{y3}$" mu_y3
a_y1
!parameters(:production :dynamic)
"Autoregression in area specific productivity component !! $\rho_\mathit{ar}$" rho_ar
"Weight on S/S inflation in inflation indexation !! $\zeta_\mathit{py}$" zeta_py
"Stage T-2 input factor adjustment cost parameter !! $\xi_{y2}$" xi_y2
"Stage T-1 input factor adjustment cost parameter !! $\xi_{y1}$" xi_y1
"Price adjustment cost parameters !! $\xi_\mathit{py}$" xi_py
rho_alpha
!shocks(:production)
"Shock to area specific productivity component" shk_ar
"Shock to final price setting" shk_py
Define substitutions
!substitutions
% Stage T-2 input factor adjustment marginal cost
adj_uk := (log(uk/y2)-log(uk{-1}/y2{-1}))-&rdf*(log(uk{+1}/y2{+1})-log(uk/y2));
adj_y3 := (log(y3/y2)-log(y3{-1}/y2{-1}))-&rdf*(log(y3{+1}/y2{+1})-log(y3/y2));
% Final price adjustment marginal cost
adj_py := log(roc_py/ref_roc_py) - beta*gg_zy*zy*log(roc_py{+1}/ref_roc_py{+1});
Define equations
!equations(:production)
%% -----Productivity-----
"Area-specific relative productivity component"
log(ar) = ...
+ rho_ar * log(ar{-1}) ...
+ (1 - rho_ar) * log(ss_ar) ...
+ shk_ar ...
!! ar = ss_ar;
%% -----Stage T-3 production: Labor and intermediate non-commodity imports-----
"Definition of variable labor input"
nv = (nh - gamma_n0*&nh) * nf;
"Stage T-3 production function"
y3 = (my/gamma_m)^gamma_m * ([ar * gg_a * nv]/(1-gamma_m))^(1-gamma_m);
"Demand for intermediate imports"
gamma_m * py3 * y3 = (pmm * gg_dmm) * my * [1 + xi_y3*($adj_mm$)] ...
!! gamma_m * py3 * y3 = (pmm * gg_dmm) * my;
"Demand for labor"
(1-gamma_m) * py3 * y3 = mu_y3 * w * nv * [1 + xi_y3*($adj_nv$)] ...
!! (1-gamma_m) * py3 * y3 = mu_y3 * w * nv;
%% -----Stage T-2 production: Variable inputs and capital-----
y2 = (uk/gamma_uk)^gamma_uk * (y3/(1-gamma_uk))^(1-gamma_uk);
gamma_uk * py2 * y2 = pu * uk * [1 + xi_y2*($adj_uk$)] ...
!! gamma_uk * py2 * y2 = pu * uk;
(1-gamma_uk) * py2 * y2 = py3 * y3 * [1 + xi_y2*($adj_y3$)] ...
!! (1-gamma_uk) * py2 * y2 = py3 * y3;
%% -----Stage T-1 Production: Add Commodity-----
%py1 = py2^(1 - gamma_mq) * pq^gamma_mq ...
py1 = alpha_y2*py2 + alpha_mq*pq ...
!! y1 = a_y1 * (y2/(1-gamma_mq))^(1-gamma_mq) * (mq/gamma_mq)^gamma_mq ...
;
"Demand for Y2 inputs"
alpha_y2 * y1 = y2;
"Demand for commodity inputs"
alpha_mq * y1 = mq;
"Input share parameter for Y2"
alpha_y2 = ...
+ rho_alpha * alpha_y2{-1} ...
+ (1 - rho_alpha) * (1-gamma_mq)*(&py1/&py2) ...
!! alpha_y2 = (1-gamma_mq)*(py1/py2) ...
;
"Input share parameter for commodity"
alpha_mq = ...
+ rho_alpha * alpha_mq{-1} ...
+ (1 - rho_alpha) * gamma_mq*(&py1/&pq) ...
!! alpha_mq = gamma_mq*(py1/pq) ...
;
%% -----T-0: Final stage production: Flatter marginal cost-----
% y + yz = (y1/(1-gamma_yz))^(1-gamma_yz) * (yz/gamma_yz)^gamma_yz;
% (1-gamma_yz) * py0 * (y + yz) = py1 * y1;
% gamma_yz * py0 * (y + yz) = py * yz;
y = y1;
py0 = py1;
yz = 1;
%% -----Final price setting-----
mu_py*py0*exp(shk_py) = py*[1 + (mu_py-1)*xi_py*($adj_py$)] ...
!! py = mu_py * py0;
ref_roc_py = roc_py{-1}^(1-zeta_py) * &roc_py^zeta_py;
pc = py;
pih = py;
%% -----Distribution of final goods-----
y = ch + cg + ih + yxx;
%% -----Rates of change-----
!for cg, pc, py, y3, nv !do
roc_? = ? / ?{-1};
!end
%% -----Definitions-----
"Per-capita private consumption"
ch_to_nn = ch / nn;
"Nominal GDP"
ngdp = pc*ch + pih*ih + pc*cg + pxx*xx - pmm*mm + pq*(xq - mq);
"Real GDP index, Y/Y"
roc_gdp = ...
+ (pc*ch/ngdp + pc{-1}*ch{-1}/ngdp{-1})/2 * roc(ch) ...
+ (pih*ih/ngdp + pih{-1}*ih{-1}/ngdp{-1})/2 * roc(ih) ...
+ (pc*cg/ngdp + pc{-1}*cg{-1}/ngdp{-1})/2 * roc(cg) ...
+ (pxx*xx/ngdp + pxx{-1}*xx{-1}/ngdp{-1})/2 * roc(xx) ...
- (pmm*mm/ngdp + pmm{-1}*mm{-1}/ngdp{-1})/2 * roc(mm) ...
+ (pq*xq/ngdp + pq{-1}*xq{-1}/ngdp{-1})/2 * roc(xq) ...
- (pq*mq/ngdp + pq{-1}*mq{-1}/ngdp{-1})/2 * roc(mq) ...
!! roc_gdp = gg_ss_roc_a * gg_ss_roc_nt;
"Per-capita real GDP index, Y/Y"
roc_gdp_to_nn = roc_gdp / roc_nn;
Postprocessing equations
!postprocessor(:production)
nch_to_ngdp = pc * ch / ngdp;
nih_to_ngdp = pih * ih / ngdp;
nkh_to_ngdp = pk * k / ngdp;
curr_to_ngdp = ($curr$) / ngdp;
!log-variables !all-but
nch_to_ngdp
nih_to_ngdp
nkh_to_ngdp
curr_to_ngdp