Wrappers

The wrappers finalize the model source codes depending on the type of the model:

• an autarky (a.k.a. closed) economy

• a multi-area economy

Autarky economy wrapper

  Algebra  Model source code

Autarky economy wrapper

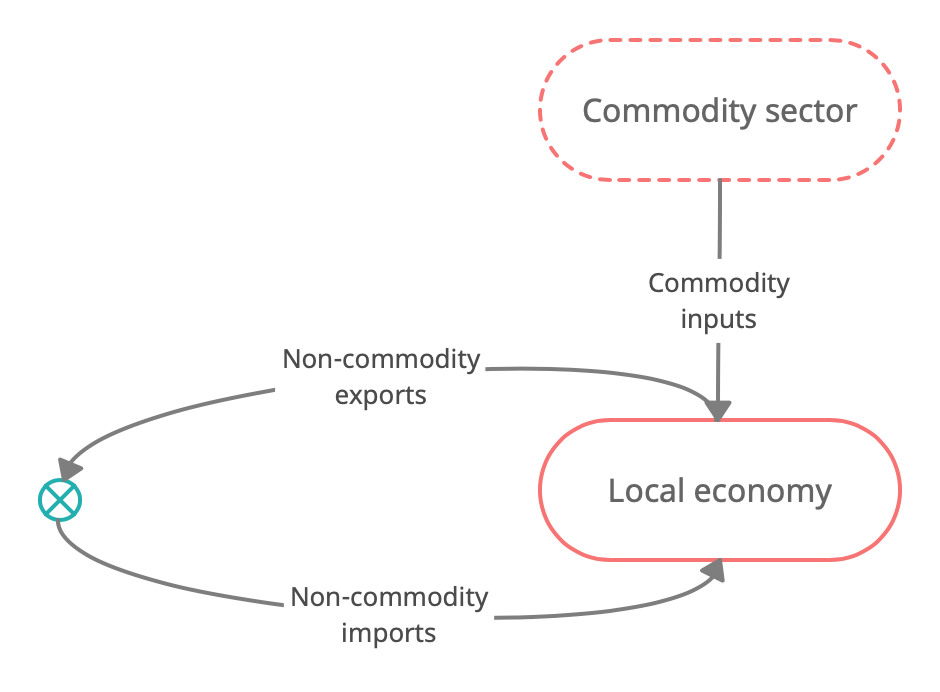
GEES Wrapper for autarky economy

Declare quantities

!variables

    "Global population" gg_nn
    "Global population, Y/Y" gg_roc_nn
    "Global index of non-commodity export prices" gg_pxx
    "Global nominal GDP" gg_ngdp
    "Global real GDP index, Y/Y" gg_roc_gdp
    "Global per-capita real GDP index, Y/Y" gg_roc_gdp_to_nn

!substitutions

    ref_k = k{+1}/&roc_k;

!parameters

    "Forward capital adjustment cost parameter" xi_k
    "Forex market functioning" zeta_r

Specify equations

!equations

    nfa_to_ngdp = 0;

    nfa_to_ngdp_checksum = 0;

    pmm = fob_pmm * (1 + trm);

    fob_pmm = pxx;

    e = 1;

    rnfa = r{-1};

    "Global population"
    gg_nn = nn;

    "Global population, Y/Y" 
    gg_roc_nn = nn / nn{-1};

    - beta*vh{+1}*rh*pk - vh*xi_k*pk*log(k/($ref_k$)) ...
        + vh*pu*u + gg_zk*zk*beta*vh{+1}*(1-delta)*pk{+1} ...
    !! - beta*vh{+1}*rh*pk + vh*pu*u + gg_zk*zk*beta*vh{+1}*(1-delta)*pk{+1};
    % !! -vh*pk + vh*pu*u + gg_zk*zk*beta*vh{+1}*(1-delta)*pk{+1} + (vh - beta*vh{+1}*rh)*pk;

    "BOP FA corporate equity transactions to GDP ratio"
    bpfeq_to_ngdp = 0;

    "BOP CA corporate equity primary income to GDP ratio"
    bpceq_to_ngdp = 0;

    "Corporate equity portfolio"
    kk = pk * k;

    "Global index of non-commodity export prices"
    gg_pxx = pxx_rcy;

    "Global demand for commodities"
    gg_q = mq;

%

%% Global GDP

    "Global real GDP, Y/Y"
    gg_roc_gdp = roc_gdp;

    "Global per-capita real GDP, Y/Y"
    gg_roc_gdp_to_nn = roc_gdp_to_nn;

    "Global nominal GDP"
    gg_ngdp = ngdp;

%

Multi-area economy wrapper

  Algebra  Model source code

$$ \newcommand{\tsum}{\textstyle\sum} \newcommand{\extern}[1]{\mathrm{\mathbf{{#1}}}} \newcommand{\local}{\mathrm{local}} \newcommand{\roc}[1]{\overset{\scriptsize\Delta}{#1{}}} \newcommand{\ss}{\mathrm{ss}} \newcommand{\aa}{\mathrm{aa}} \newcommand{\bb}{\mathrm{bb}} \newcommand{\E}{\mathrm{E}} \newcommand{\ref}{{\mathrm{ref}}} \newcommand{\blog}{\mathbf{log}\ } \newcommand{\bmax}{\mathbf{max}\ } \newcommand{\bDelta}{\mathbf{\Delta}} \newcommand{\bPi}{\mathbf{\Pi}} \newcommand{\bU}{\mathbf{U}} \newcommand{\newl}{\\[8pt]} \newcommand{\betak}{\mathit{zk}} \newcommand{\betay}{\mathit{zy}} \newcommand{\gg}{\mathrm{gg}} \newcommand{\tsum}{\textstyle{\sum}} \newcommand{\xnf}{\mathit{nf}} \newcommand{\ratio}[2]{\Bigl[\textstyle{\frac{#1}{#2}}\Bigr]} \newcommand{\unc}{\mathrm{unc}} \notag $$

Symmetric two-area economy wrapper

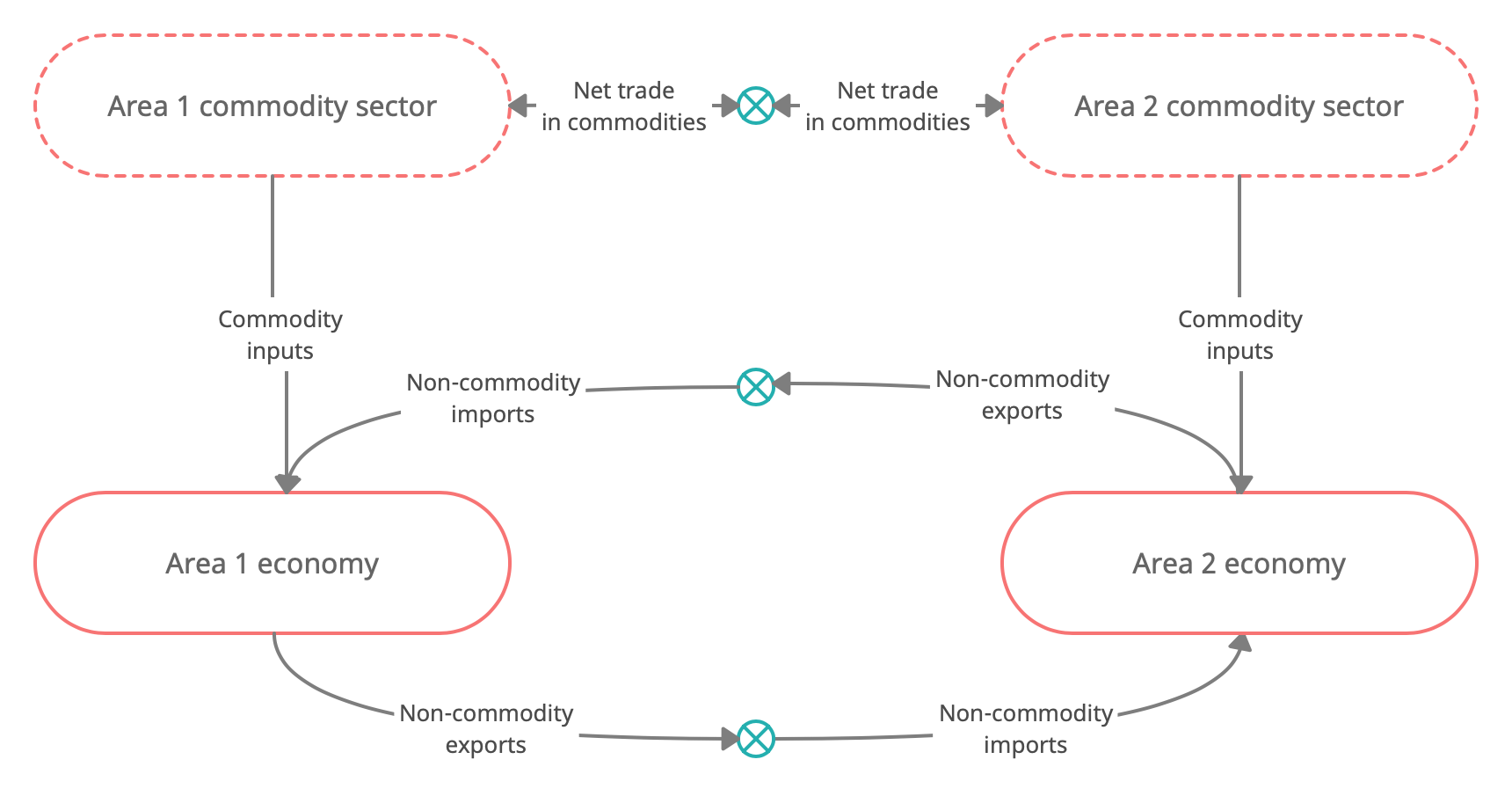
Determination of interest rates in the long run

• Example of a two-area setup

• Assume zero inflation in either area for simplicity (hence, nominal interest rates equal real interest rates)

• With zero inflation differentials and equal long-rung productivity growth (driven by the global productivity growth)

• Initially, we turn off the net worth effect by setting \(\nu_1=0\)

Interest parity (international debt finance markets) in base rates

\[ r^\aa = r^\bb \]

Effective household rate (local banking sector)

\[ \begin{gathered} rh^\aa = r^\aa + f\left(\frac{\mathit{nfa}}{\mathit{ngdp}}\right) \\[5pt] rh^\bb = r^\bb + f\left(\frac{\mathit{nfa}}{\mathit{ngdp}}\right) \end{gathered} \]

Euler equations (consumer choice)

\[ \begin{gathered} rh^\aa = \frac{1}{\beta^\aa} \, \roc{a^\gg} \\[5pt] rh^\bb = \frac{1}{\beta^\bb} \, \roc{a^\gg} \end{gathered} \]

• Effective real interest rates are determined by the discount factor, \(\beta\), and real growth, \(\roc{a}\).

• The space between the base rate and the effective rate is filled with a premium/spread determined by the NFA position in each area

GEES Wrapper for multi-area economy

Declare quantities

!variables

    "Global population" gg_nn
    "Global population, Y/Y" gg_roc_nn
    "Global index of non-commodity export prices" gg_pxx
    "Global nominal GDP" gg_ngdp
    "Global real GDP index, Y/Y" gg_roc_gdp
    "Global per-capita real GDP index, Y/Y" gg_roc_gdp_to_nn

!parameters
    !for ?A=<areas(2:end)> !do
        "Forex market functioning" ?A_zeta_r
    !end

Define equations

!equations

Multi-area equilibrium and clearing

    "Net asset clearing"
    0 = !for ?A=<areas> !do + ?A_nfa_to_ngdp * ?A_ngdp / ?A_e !end;

    !for ?A=<areas(2:end)> !do
        "Interest parity"
        ?A_rip = <areas(1)>_rip * (?A_exp_e / ?A_e * exp(?A_shk_e))^(1/?A_zeta_r) * (&?A_roc_e)^(1-1/?A_zeta_r);

        "Effective NFA rate"
        ?A_rnfa = <areas(1)>_r{-1} * ?A_e / ?A_e{-1};

        "NFA checksum"
        ?A_nfa_to_ngdp_checksum = 0;
    !end

    "Global reference currency effective NFA rate"
    <areas(1)>_rnfa = <areas(1)>_r{-1};

    "Reference currency exchange rate"
    <areas(1)>_e = 1;

    "Global population"
    gg_nn = !for ?A=<areas> !do + ?A_nn !end;

    "Global population, rate of change"
    gg_roc_nn = gg_nn / gg_nn{-1};

    "Global index of non-commodity export prices"
    gg_pxx = ...
        (!for ?A=<areas> !do + ?A_pxx_rcy * ?A_nxx_rcy !end) ...
        / (!for ?A=<areas> !do + ?A_nxx_rcy !end) ...
    ;

    "Global demand for commodities"
    gg_q = !for ?A=<areas> !do + ?A_mq !end;

Global GDP

    "Global nominal GDP"
    gg_ngdp = !for ?A=<areas> !do + ?A_ngdp_rcy !end;

    "Global real GDP, Y/Y"
    gg_roc_gdp = ...
        !for ?A=<areas> !do + (?A_ngdp_rcy/gg_ngdp + ?A_ngdp_rcy{-1}/gg_ngdp{-1})/2 * ?A_roc_gdp !end;

    "Global per-capita real GDP, Y/Y"
    gg_roc_gdp_to_nn = gg_roc_gdp / gg_roc_nn; 

International comparison

!for ?A=<areas> !do
    !variables
        "Nominal GDP, Reference currency [?A]" ?A_ngdp_rcy
        "Per-capita private consumption" ?A_comp_ch_to_nn
        "Per-capita gross production" ?A_comp_y_to_nn
    !equations
        ?A_ngdp_rcy = ?A_ngdp / ?A_e;
        ?A_comp_ch_to_nn = (?A_ch / ?A_nn) / (<areas(1)>_ch / <areas(1)>_nn);
        ?A_comp_y_to_nn = (?A_y / ?A_nn) / (<areas(1)>_y / <areas(1)>_nn);
!end